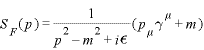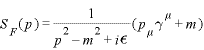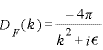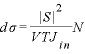概略

注意
QEDのコーナーは全て自然単位系を用いています

ここでの話は場の量子論でもう一度定式化しているので、見ないで場の量子論に行っても問題はありません。
また、ここではほとんど代数的な計算に費やされているので、そんなものはどうでもいいという人も飛ばしていいです。今は、mathemathica等の計算ソフトでガンマ行列の計算とかできるので、手でやる必要性は大分なくなってきています。

相対論的量子力学では主にディラックの理論についての説明をしてきましたが、ここではQED(量子電磁気学,量子電気力学)と呼ばれているものの説明に入ります。QEDは相対論的量子力学を使った電磁相互作用の話です。つまり、QEDは電子(レプトン)の相互作用による散乱(断面積)について考えます。
相対論的量子力学の範疇に入っているので、これも特殊相対論を量子論に組み込んだもので、使う方程式はディラック方程式になります。ディラック方程式はスピン1/2の粒子を記述するものということは忘れないでください。

というわけで、ディラックの理論から電子の散乱問題を解いていこうとすると、いきなり壁にぶち当たります。なぜかというと、ディラックの理論の成果であるディラックの海が問題を複雑化させてしまうからです。ディラックの海の存在を仮定することは、電子1個について考えてるだけなのに、それに付随するように負エネルギーで埋められた海が影をちらつかせ、多体問題にさせてしまうからです。だったら仮定しなければいいと言うことはできなく、仮定しないと散乱によって電子は負エネルギーに落ちていってしまいます。

こういった厄介な状況を打破したのがファインマン達です。何をしたのかというと、負エネルギーを持った粒子は時間を逆行するというSF小説みたいな発想を持ち出してきました。

この発想の前に、Stueckelbergの粒子に対する因果律というものがあって、粒子はまず生成されてから消滅するという因果律を持つとされ、これに対して負エネルギー粒子は変な振る舞いをしていると考えられました。
陽電子(反粒子)が生成されることはディラックの海に空孔ができることに対応しています。これの意味は、負エネルギー電子が消滅したということです。そして、この陽電子が消滅することは負エネルギー電子が生成されることを意味しています。
つまり、陽電子の生成、消滅に対して負エネルギー粒子は消滅してから生成されることになります。負エネルギー粒子は粒子に対する因果律をものの見事に破っていることになるので、負エネルギー粒子は粒子ではないという解釈をStueckelbergはしました。なんとなく屁理屈みたいな論理ですが、ディラックの海による陽電子生成について考えれば何も変なことは言ってないです。

このことからファインマンの発想は、負エネルギー粒子は実際の粒子じゃないんだから別に時間を逆行してても何の問題もないじゃないか、と言ってるようなものです。実際に何の問題もないことが示されています。
このファインマンの負エネルギー粒子は時間を逆行するものである、ということを導入してやると、ディラックの海の存在を表面上無視して理論を展開していけます。簡単に言うと、正エネルギーは正エネルギー領域だけで時間通りに振舞って、負エネルギーは負エネルギー領域だけで時間を逆行するというものになります。

こういった理論の中心にあるものが、ファインマンの伝播関数、数学ではグリーン関数と呼ばれているものです。これを使うことで散乱による影響を含んだ波動関数を求めることができるようになります。
ここで使う伝播関数は電子と光子の伝播関数で

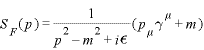
　　　　　 $S_{F}(p)=\displaystyle \frac{1}{p^{2}-m^{2}+i\epsilon}(p_{/}+m)$

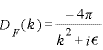
　　　　　 $D_{F}(k)=\displaystyle \frac{-4\pi}{k^{2}+i\epsilon}$

これは運動量表示のものですが、座標表示のものを使ったりもします。なんで光子が出てくるのかというと、電磁場による相互作用は光子によって行われているからです。
こういった伝播関数を使って散乱(電子と陽子とか)の問題を解いていきます。基本的にはS行列と呼ばれる遷移振幅を求めて、微分断面積を求めていくことになります。S行列と断面積を結ぶ式は

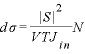
　　　　　　 $d\displaystyle \sigma=\frac{|S|^{2}}{VTJ_{in}}N$

のようになっています。Vは体積、Tは時間、Jは入射粒子の速度、Nは終状態の数。Nの部分はVとあわせて密度化させて使ったりもします。

こうやって散乱問題を解いていくと、例えばクーロンポテンシャルによる電子の散乱はラザフォード散乱と呼ばれ、ラザフォードの散乱公式を導けます。他にもコンプトン散乱では有名なクライン・仁科の公式を導けたりもします。また、問題を解くときにファインマン図と呼ばれるものを書くことで、視覚的に格段に簡単になります。

QEDは主に摂動論によって答えを求めていくので、1次のオーダーや2次のオーダーならまだいいですが、高次のオーダーになってくるにつれて手間は可笑しくなるほど増加していきます。その上、理論の作る上でも重要なことですが、積分が発散するという致命的なことが起きます。発散する原因は3つあって、真空偏極(vaccum polarization)、自己エネルギー(self−energy)、頂点関数(vertex correction)と呼ばれていて、これらを含むものは発散します。

この発散をどうするかが現在でも重大な問題になっていて、これは場の量子論においても大問題になっています。これを一応は突破したのが、くり込み(renormalization)と呼ばれるもので、発散部分を観測可能な物理量にくり込んでしまえというものです。こうすることで発散部分なんか存在してないとしています。一種の詐欺みたいなものです。それでもディラック方程式で水素原子を解いたときに生じるズレ(ラム・シフト)を見事に説明し、測定との誤差が異様に小さい結果を導いています。このくり込みの成果がQEDの最大の成果ともいえるものです。

QEDの概略を言ってきましたが、実際に散乱の計算を行うと、積分の計算やら、トレースの計算やら、とんでもなく面倒になっています。なので、真面目に触れようと思うとえらい時間と労力が必要なので気をつけてください。また、QEDも場の量子論に移行させる必要がありますが、行っている計算は同じです。

戻る