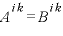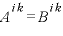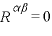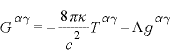イントロ
一般相対性理論の発想が出てくるまでの話はごちゃごちゃしているので飛ばします。一般相対性理論を一言で言えば現在最も有用な重力理論ということです。また、一般相対性理論が美しい理論と呼ばれるのは、基本要請から一直線に構成されているためです。
大雑把に一般相対性理論の概要を言えば、曲がった空間を4次元のリーマン幾何学で表現する、物体は曲がった空間上の最短距離(測地線)を進む、曲がった空間はアインシュタイン方程式によって記述される、というものです。
一般相対性理論では曲がった空間を扱うためのリーマン幾何学とそこで使用されるテンソルがやっかいな存在になっています。量子論の入門的な部分は力学や電磁気と大差ない数学で記述されているために、物理的な意味や概念がわかりづらくても、後半にならない限り数学で苦労することはあまりないはずです。しかし、一般相対性理論では数学の準備から始めなくてはならない上に、その数学が格段に分かりづらくなっています。数学としてちゃんとリーマン幾何学を理解しようと思ったらそれだけで力尽きそうになるような内容です。
しかし、よっぽど本格的に一般相対性理論をやろうと思わない限り雑に暗記しておくだけでどうにか出来ます(何にしても計算はひどく面倒)。
一般相対性理論でテンソルが必要になる理由は座標系に依存しない記述がしたいからです。例えば、当たり前のようですが
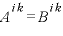
という関係が適当な座標系で成り立っていたとしたら、この関係は他のどんな座標系においても維持されます。このように、テンソル形式の式は一般相対性理論の座標系に依存しないという要請を満たします。つまり、テンソル(共変な形)であればあらゆる座標系にその関係は適用できます。アインシュタイン方程式はテンソル形式の方程式です。
一般相対性理論での必要最低限の知識は、クリストッフェル記号、共変微分、リーマン曲率テンソル、測地線方程式です。後は特殊相対性理論の知識があればアインシュタイン方程式がどういうものなのか分かります。また、計算を行う上では背後にある空間が曲がっているという考えは、物理を考えない限り数学の中に閉じ込められてしまい意識する必要がなくなります。
ちなみに、計量に対する方程式なので分かりづらいですがアインシュタイン方程式は場の方程式であって、一般相対性理論は(古典的な)場の理論です。
物質が何もない場合でのアインシュタイン方程式は
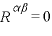
と与えられ、Rが曲率を表すリーマン曲率テンソルです。有名なシュバルツシルト解は物質の何もない場合でのアインシュタイン方程式によって導かれます。
これに物質がある場合として求まるものがアインシュタイン方程式と一般に呼ばれる方程式
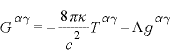
Gはアインシュタインテンソルと呼ばれ、リーマン曲率テンソルによって表現されるものです。Tはエネルギー・運動量テンソル、Λは宇宙項と呼ばれます。左辺が空間の曲がり具合を、右辺が空間の歪みの源となる物質(エネルギー)を表しています。また、アインシュタイン方程式の解は空間の計量です。
ここでの計量の符号の注意もしておきます。ここでは、ミンコフスキー空間での計量を
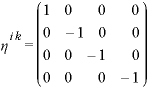
としています。(−,+,+,+)の方が三次元空間が+になっていて便利なんですが、ここではこっちの定義を使います。また、ミンコフスキー空間は平坦なので、これにれに摂動項を加えることで、重力が弱い時の計量を作れます。
相対性理論が生き残っているのは、実験結果と一致しているためです。物理は基本的には実験結果(現実の現象)が最初にありそこから理論が作られていくものなので、現実と合う限りそれは正しい理論として扱われます。また、思考実験で上手くいったからといってそれが現実を表現する正しい理論になるとは限らないですが、相対性理論(量子論もですが)の致命的なところは現実の実験ができず、思考実験しかできない領域があることです。なので、たとえ相対性理論の原理が間違っているとして組み立てた理論でもそれが相対性理論以上に現実を綺麗に表現していれば、そちらに取って代わられます。しかし、今のところそのような理論は認められていない(ほぼ観測結果待ちで今のところ相対性理論に致命的な問題が起きていない)ので相対性理論が宇宙を記述する中心的役割を担っています。
また、物理は現象と数学の兼ね合いなので、日常感覚がどこまでも成立していると思うか、数学の記述を信じるか、というのでも立場が変わります。ようは、人間が日常的に体験できる現象のみで世界が成り立っているのかどうかというだけです。極端な例では、量子論において観測の限界の内側ではどうせ観測できないから何が起きていても良いという立場をとる人もいます。
言葉の問題でしかないです、ニュートンの理論を相対性理論から見て古典論と言う時もあります。しかし、一般的には量子論以外を古典論と呼ぶので、この使い方はしないほうがいいです。
戻る