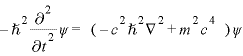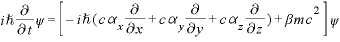概略
ここでは主にディラック方程式の説明をしています。QEDや場の量子論のための準備程度にしか作っていないので、あまり細かいことには触れていません。
とっとと先に進みたい人は、「クライン・ゴルドン方程式」、「ディラック方程式」、「空孔理論」、「ディラック方程式~共変性~」の前半、「射影演算子」を見ればいいです。
通常の量子力学において自由粒子のエネルギーは
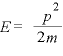 … (1)
… (1)
という関係を基本としています。これを相対論的エネルギーに拡張してやることから始まります。ついでに当たり前ですが、3次元から4次元へとも拡張されることになります。つまり、相対論的な観点からは、今までの量子論では運動量(速度)が小さいという非相対論近似において成り立っていたものだということになります。
というわけで、このエネルギーを相対論的エネルギーで表すと
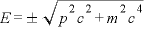
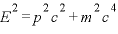 … (2)
… (2)
ここで、自由粒子のシュレーディンガー方程式は簡単に言ってしまえば、(1)のEとPを演算子に書き換えることで作ることができます。なので(2)でも同じことをすれば、相対論におけるシュレーディンガー方程式というものを作れることになり、それをクライン・ゴルドン(Klein−Gordon)方程式と呼んでいます。それを書くと
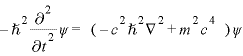
という形になっています。ちなみに、クラインとゴルドンの名前がついていますが、他にも何人か同じ方程式を同時期に導出しています。
これで、量子論を相対論的に扱えるようになったかのように思えますが、そう簡単にいかなく、この方程式には問題点が存在しています。それは、量子論において重要な性質である確率解釈において現れます。簡単にいってしまえば、負の確率というわけのわからないものが計算結果として求められてしまう点です。この負の確率が現れるのは、(2)を見れば分かるように、相対論におけるエネルギーには±の二つが存在しているからです。その負エネルギーの存在のせいで確率が負になってしまいます。さらに、この負エネルギーには問題があって、現実の粒子には安定を求めてより可能な低いエネルギーへと行こうとする性質があるために、負エネルギーを許してしまうと粒子は負エネルギーへとエネルギーを放出しながらどんどん落ちていってしまい、この世界が存在できなくなります。
こういった問題は単純に負エネルギーを無視すればいいように思えますが、負エネルギー解を無視してしまうと今度は数学的に成り立たなくってしまうので簡単に無視することができないです。このようにクライン・ゴルドン方程式の解釈は難しくなっており、この式による正確な記述をするためには場の量子論への発展が必要になります。
クライン・ゴルドン方程の問題を解決するために、ディラックによってディラック方程式が導入されました。
改良の目的ははっきりしていて、クライン・ゴルドン方程式の問題点は時間による2階微分が入っているせいと考えて、この部分を書き直してやるというものです。なぜこれが問題なのかというと、この2階微分のせいで初期条件として、波動関数とその1階微分の値を任意に選べるという点です。
というわけで時間微分を1階に直しますが、それに伴って共変性を保つために空間微分も1階になっている必要があると推測されます(実際に求めてやれば1階でないと成り立たないのがわかる)。
というわけでこの発想に従うディラック方程式は
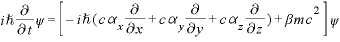
このようになる必要があります。αとβはまだ適当な数です。
で、この式は当然ながら、二乗したときにクライン・ゴルドン方程式を満たしていなければならないので、その関係からαとβが満たすべき関係が求まることになります。なのでαとβというのははっきりと決まったものとはならず、状況によって違ったものが使われます。
そして、αとβがどんなものなのかは計算してやると4×4行列であることがわかり、パウリ行列を使って表せます。その関係上、波動関数も4成分をもっていることが要求されます。
というわけで、ディラック方程式は4×4行列と4成分の波動関数を含むという、計算上えらい迷惑なものになっています。さらに、このディラック方程式で記述されているものは電子、より広く言えばスピン1/2をもった粒子となっていて、スピンという概念が方程式の性質として最初から含まれています。
この方程式では、確率解釈は非相対論での量子論と同様に扱えるので、負の確率問題は解消されます。しかし、まだ負エネルギー解は依然として存在しているので、この問題も解決してやらないといけません。また、クライン・ゴルドン方程式もディラック方程式も一粒子状態しか記述できないので多粒子状態を扱うことができません。
こういった中でディラックは空孔理論(Hole Theory)なるものを提唱しました。それは簡単にいえば、真空とは負エネルギー解によって満たされていて(ディラックの海)、粒子はそこに落ちていけないという条件をつけるというものです。ただの仮定にすぎない発想ですが、これによって反粒子の存在を予言でき、反粒子の存在は実験的に確かめられています。
これが相対論的量子力学の大まかな内容です。空孔理論にもいろいろ問題点があり、さらに正確な理論を求めるために場の量子論へと進んでいくことになります。
戻る
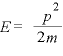 … (1)
… (1)
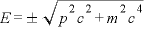
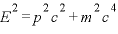 … (2)
… (2)